Neuronske mreže > Predavanje > 

4. Na koji način se učenjem stvara neuronska mreža?

Rad umjetne neuronske mreže odvija se u dvije osnovne faze: najprije se odvija faza učenja ili treniranja mreže, a zatim slijedi faza testiranja.

Animacija 4. Kako se korigira znanje u jednoj neuronskoj mreži.

1) Učenje
Učenje je proces mijenjanja težina u mreži, a odvija se kao odgovor na podatke izvana koji su predstavljeni ulaznom sloju i u nekim mrežama izlaznom sloju. Podaci koji se predstavljaju izlaznom sloju su željene vrijednosti izlaznih varijabli. Ukoliko su one poznate, radi se o tzv. nadgledanom učenju. Na primjer, nadgledani algoritmi su: mreža širenje unatrag, mreža s radijalno zasnovanom funkcijom, modularna mreža, vjerojatnosna mreža, LVQ (mreža učeće vektorske kvantizacije), i drugi. Ukoliko je ulazni vektor jednak izlaznom vektoru, radi se o autoasocijativnim mrežama, a ukoliko je različit, radi se o heteroasocijativnim mrežama. Kod nekih mreža željeni izlaz ne mora biti predstavljen mreži. U tom slučaju radi se o tzv. nenadgledanom učenju. Najčešći nenadgledani algoritmi su Kohonenova mreža, mreža konkurentskog učenja, te ART (mreža adaptivne rezonantne teorije).

Prije samog učenja potrebno je definirati model (ulazne i izlazne varijable), te prikupiti podatke iz prošlosti na kojima će se primijeniti mreža. Prikupljene podatke treba podijeliti u dva poduzorka (uzorak za treniranje i uzorak za testiranje), a ukoliko se za vrijeme učenja planiraju koristiti optimizacijske tehnike za optimiranje duljine učenja i strukture mreže, potrebno je ukupan uzorak podijeliti na tri poduzorka (za treniranje, testiranje i konačnu validaciju). Pravila za ovu podjelu nema, osim što se preporuča najveći dio podataka ostaviti za treniranje mreže, a manji dio podataka za testiranje i validaciju (npr. 70% za treniranje, 10% za testiranje i 20% za validaciju). Podaci se raspoređuju u poduzorke slučajno, osim kod vremenskih serija gdje treba poštovati vremenski slijed nastajanja promatranja, tj. trenirati mrežu na starijim, a testirati na novijim podacima.

Nakon što je definiran model, pripremljeni ulazni podaci i izabran NM algoritam, te pravilo učenja i potrebne funkcije, mrežu treba učiti ili trenirati na pripremljenim podacima iz prošlosti, kako bi ona prepoznala vezu između podataka i bila u mogućnosti na osnovu ulaznih vrijednosti predviđati izlaze. Sama faza učenja je proces podešavanja težina u mreži, koje se odvija u više iteracija ili prolaza kroz mrežu. Jedna iteracija predstavlja učitavanje jednog promatranja iz podataka (jednog ulaznog i izlaznog vektora), ali se zbog povećanja brzine učenja ponekad preporuča učitati više promatranja odjednom, pri čemu se broj promatranja koji se obrađuju u jednoj iteraciji zove epoha. U svakoj iteraciji računaju se nove težine, a kod nadgledanih algoritama i nova greška. Obično se mreža trenira u nekoliko tisuća iteracija.

Najvažnije pitanje u ovoj fazi je koliko dugo trenirati mrežu kako bi ona dala što bolji rezultat, odnosno najmanju grešku. Ne postoje egzaktna pravila za dužinu treniranja, te odgovor na ovo pitanje treba potražiti vlastitim eksperimentiranjem ili primjenom optimizacijskih tehnika kao npr. tehnika unakrsnog testiranja. Ova se tehnika može opisati u nekoliko koraka:

• mreža se najprije trenira na određenom broju iteracija (npr. 10000),
• tako naučena mreža se testira na uzorku za testiranje, i pohrani dobiveni rezultat i mreža.
• mreža se zatim nastavlja trenirati na još tolikom broju iteracija (npr. još 10000), te se dobiveni rezultat uspoređuje s prethodno pohranjenim. Ukoliko je u ponovnom učenju dobiven bolji rezultat, pohranjuje se novi rezultat i nova mreža.
• postupak se ponavlja sve dok se rezultat prestane poboljšavati, a najbolja pohranjena mreža ulazi u daljni postupak validacije.
  

Rezultat (npr. RMS greška) dobiven u fazi učenja nije mjerodavan za ocjenjivanje mreže, jer ne pokazuje ponašanje mreže na novim podacima.

2) Testiranje mreže
Testiranje mreže je druga faza rada neuronske mreže, i ona je odlučujuća za ocjenjivanje mreže. Razlika između faze učenja i faze testiranja je u tome što u ovoj drugoj fazi mreža više ne uči, a to znači da su težine fiksne na vrijednostima koje su dobivene kao rezultat prethodne faze učenja. Takvoj mreži se predstavljaju novi ulazni vektori koji nisu sudjelovali u procesu učenja, a od mreže se očekuje da za predstavljen novi ulazni vektor proizvede izlaz. Ocjenjivanje mreže obavlja se izračunavanjem greške ili nekog drugog mjerila točnosti (npr. stope točnosti), na način da se izlaz mreže uspoređuje sa stvarnim izlazima.

Dobivena greška mreže na uzorku za validaciju je rezultat kojim se tumači uspješnost ili neuspješnost neuronske mreže i njezina korisnost u primjeni za predviđanje na budućim podacima. Najčešća greška koja se računa kod neuronskih mreža je srednja kvadratna greška (Root mean square error), prema formuli:

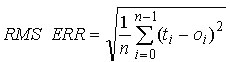
gdje je ti  izračunati izlaz koji daje mreža, oi  je željeni (stvarni) izlaz za slučaj (ulazni vektor) i, a n je broj slučajeva u uzorku. Greška se uprosječuje prema broju izlaznih varijabli i u odnosu na broj slučajeva u uzorku na kojem se računa. Kod problema klasifikacije se u većini istraživanja koristi stopa klasifikacije kao mjerilo ocjenjivanja mreže. Stopa klasifikacije prikazuje postotak ili udio ispravno klasificiranih promatranja. Kod problema predviđanja najčešće se kao mjerila koriste RMS greška, MSE (Mean Square Error), MAE (Mean Absolute Error), koeficijent korelacije i dr.), dok se u novije vrijeme (Masters, 1998) posebno kod financijskih problema naglašava potreba korištenja financijskih mjerila (npr. ostvareni simulacijski profit, prosječni profit i sl.).

U slučaju upotrebe više NM algoritama, potrebno je na osnovu rezultata na uzorku za validaciju mreže donijeti konačnu ocjenu o najboljem modelu NM za dani problem. Mjerila na osnovu kojih se ova odluka donosi ovise o tipu problema (predviđanje vs. klasifikacija), prirodi problema (da li je profit ostvaren upotrebom mreže značajniji od veličine njezine greške), i sl.

Process dizajniranja neuronske mreže sastoji se od nekoliko faza: (1) definiranje modela (izbor ulaznih i izlaznih varijabli, priprema ulaznih podataka), (2) izbor najprikladnijeg algoritma (npr. backpropagation), (3) raspoređivanje neurona u slojeve (izbor broja skrivenih slojeva, te broja neurona u svakom skrivenom sloju), (4) određivanje tipa veze među neuronima, te ulaznih i prijenosnih funkcija između slojeva, (5) izbor pravila učenja, te nekih parametara učenja, npr. koeficijenta učenja i momentuma koji utječu na brzinu i kvalitetu učenja, (6) izbor mjerila za ocjenjivanje mreže (npr. RMS greška ili stopa klasifikacije), i (7) provođenje postupka učenja.

Animacija 5. Kako se dizajnira umjetna neuronska mreža

Ovisno o temeljnim formulama koje se koriste za učenje, ulazne i izlazne funkcije, postoje različiti algoritmi NM, a unutar svakog algoritma moguće su intervencije u strukturi mreže (topologiji) i izboru parametara učenja, te tako postoji široki spektar NM arhitektura. One se međusobno razlikuju prema kriterijima:

• broju slojeva (dvoslojne i višeslojne),
• tipu veze između neurona (inter-slojne veze i intra-slojne veze),
• vezi između ulaznih i izlaznih podataka (autoasocijativne i heteroasocijativne),
• ulaznim i izlaznim (prijenosnim) funkcijama,
• pravilu učenja,
• ostalim parametrima (sigurnosti ispaljivanja, vremenskim karakteristikama, i dr.).

Od gore navedenih karakteristika, za razlikovanje algoritama od osobitog je značenja pravilo učenja. Pravilo učenja specificira način na koji se podešavaju težine u mreži. Objasnit ćemo način podešavanja težina na jednostavnom Delta pravilu, koje je jedno od prvih razvijenih pravila učenja za neuronske mreže.

	Slika 6. a) Računanje greške neuronske mreže
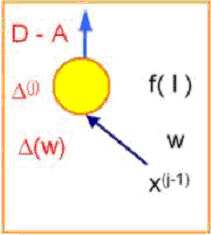
b) računanje greške neurona u izlaznom sloju	c) korekcija težina veza neurona u izlaznom sloju
d) računanje greške neurona u skrivenim slojevima	e) korekcija težina veza neurona u izlaznom sloju

Težina veze w  je jačina veze između dva neurona. Ako je, na primjer, neuron j  povezan s neuronom i, wji  označava težinu veze od neurona j  prema neuronu i (wij  je težina obrnute veze od neurona i prema neuronu j). Ako je neuron i  spojen s neuronima 1,2,...,n, njihove težine su pohranjene u varijablama w1i, w2i, ..., wni. Promjena težina obavlja se prema nekom od pravila učenja, a najčešće se koristi Delta pravilo učenja prema formuli:

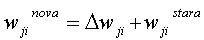
gdje je vrijednost prilagođavanja težine veze od neurona j  prema neuronu i  izračunatom prema:

,

gdje je ycj  vrijednost izlaza izračunatog u neuronu j, ei  je sirova greška izračunata prema:

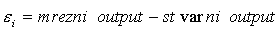
a h  je koeficijent učenja. Neuron prima onoliko ulaza koliko ima ulaznih veza prema tom neuronu, te proizvodi jedan izlaz u skladu s ugrađenom prijenosnom funkcijom.

U izlaznom sloju izlaz mreže uspoređuje se s željenim (stvarnim) izlazom, i određuje se globalna greška E kao:

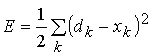
gdje je dk  željeni (stvarni) izlaz, dok je xk  izlaz mreže, a k  je indeks izlazne komponente, tj. broj izlaznih jedinica. Svaka izlazna jedinica ima vlastitu lokalnu grešku e  čiji je sirov oblik (dk-xk), ali ono što se propagira kroz mrežu je skalirana greška u obliku gradijent komponente:

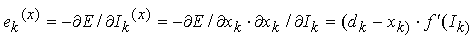
Cilj procesa učenja u mreži "širenje unatrag" je minimizirati gornju globalnu grešku šireći je unazad u veze kroz mrežu sve do ulaznog sloja. U procesu mijenjanja težina, svaka veza u mreži korigira se kako bi se postigla manja globalna greška. Proces povećanja ili smanjenja težina (učenje) izvodi se korištenjem pravila gradijentnog opadanja:

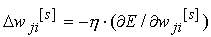
gdje je h koeficijent učenja. Da bi se izračunale parcijalne derivacije u gornjoj jednadžbi, što daje:

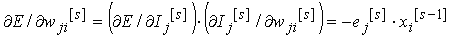
Kada se gornji rezultat uvrsti u formulu za podešavanje težina, dobiva se:

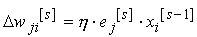
što vodi do glavnog problema postavljanja odgovarajuće stope učenja. Postoje dvije međusobno konfliktne smjernice za određivanje h. Prva smjernica je održavati h na niskoj vrijednosti jer ona određuje područje u kojem je površina greške lokalno linearna. Ako mreža pretendira predvidjeti jaku zakrivljenost, takvo područje trebalo bi biti vrlo malo. Međutim, vrlo mali koeficijent učenja znači vrlo sporo učenje. U cilju rješavanja ovog sukoba, prethodne razlike težina u vremenu (t-1) dodane su u prethodnu jednadžbu, tako da je trenutno podešavanje težina:

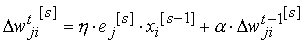
gdje je momentum, koji ubrzava učenje kada je koeficijent učenja nizak. Učenje se može također ubrzati na način da se težine ne podešavaju za svaki vektor treniranja, nego kumulativno, pri čemu se broj vektora treniranja nakon kojeg se težine podešavaju zove epoha. Epoha koja nije jako velika može unaprijediti brzinu konvergiranja, ali vrlo velika epoha može računanje greške učiniti mnogo složenijim i na taj način umanjiti prednosti.

Primjer 3. Izračun korekcije težine veze neurona br. 5 prema izlaznom neuronu br. 6

Jedna od najčešće primjenjivanih neuronskih mreža svakako je mreža "širenje unatrag" ili (eng. backpropagation), te će u nastavku biti opisano funkcioniranje neuronskih mreža na tom algoritmu.

3. Obrada informacija u neuronskoj mreži ... 5. Mreža "širenje unatrag"

13.03.2003