|
Neuronske mreže
> Predavanje
>
| 3. Obrada informacija
u neuronskoj mreži |
U umjetnoj neuronskoj mreži obrada se informacija
također izvodi u jedinicama koje zovemo neuronima ili elementima
za obradu. Izraz neuron označava osnovnu jedinicu u modelu neuronske
mreže koja je namijenjena obradi podataka (zbog toga su izrazi
"jedinica obrade" ili "elementi za obradu"
korišteni često kao sinonimi za neuron). Umjetni neuron također
ima više ulaza od kojih prima informacije (oni su analogni dendritima
kod živih neurona), zbraja ih s pomoću neke zbrojne funkcije
i tako stvara svoju internu aktivaciju. Zatim se u neuronu s
pomoću funkcije prijenosa mijenja taj zbrojni ulaz. Funkcija
prijenosa može biti diskontinuirana funkcija skoka, ili neka
kontinuirana funkcija, kao npr. sigmoida ili tangens-hiperbolna
funkcija.
Animacija
2. Što se događa u jednom neuronu.
Pokazat ćemo kako se obrađuju informacije na neuronskoj mreži
koja se naziva širenje unatrag (engl. Backpropagation). Ta mreža
se intenzivno upotrebljava za različite klase problema te ima
jednostavan model koji se može lako opisati i naučiti.
Matematički model obrade informacija u računalnom neuronu je
slijedeći. Ulazi u neurone indeksirani sa i = 1, ..., n primaju
ulazne vrijednosti xi. Ulazne vrijednosti neki su realni
brojevi. Svaka ulazna vrijednost xi množi se s težinskom vrijednošću
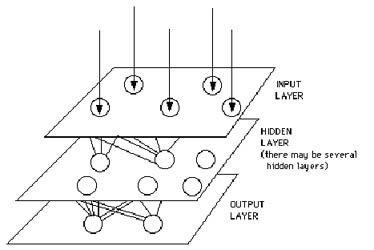
wi. Zbroj S svih ponderiranih veličina zove se interna aktivacija
I. Ona je jednaka:
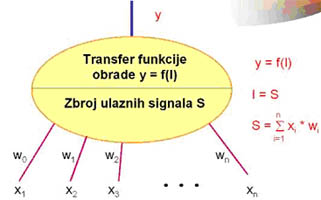 |
Slika
3. Prikaz računalnog neurona
|
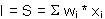
Tako dobiven zbroj S (ili
interna aktivacija I) obrađuje se pomoću funkcije obrade f.
Izlaz iz neuronske mreže jednak je y:
y
= f(I)
Primjer
1. Primjer obrade informacija u jednom neuronu.
Neuroni su spojeni u mrežu
na način da izlaz svakog neurona predstavlja ulaz u jedan
ili više drugih neurona. Prema smjeru, veza između neurona
može biti jednosmjerna ili dvosmjerna, a prema intenzitetu
moguća je pobuđujuća (egzitatorna) ili smirujuća (inhibitorna)
veza. Neuroni su obično u umjetnoj neuronskoj mreži organizirani
u grupe ili slojeve u kojima se informacije paralelno obrađuju.
Tipična neuronska mreža sastoji se od nekoliko slojeva, najčešće
dva vanjska, te od jednog ili više međuslojeva ili tzv. skrivenih
slojeva (slika 4). Vanjski slojevi su: ulazni sloj koji učitava
podatke iz okoline i izlazni sloj koji prikazuje rezultat
mreže za zadani ulaz. Upravo je skriveni sloj onaj u kojem
se uče međuzavisnosti u modelu, informacije neurona se ovdje
obrađuju i šalju u neurone izlaznog sloja.
Animacija
3. Što se događa između neurona u mreži.
|
Slika 4. Neuronska mreža
|
|
|
|
Slika
5. Prikaz neurona
s oznakama koje objašnjavaju njegov smještaj u mreži.
|
Kada ulazni sloj šalje
podatke u prvi skriveni sloj, svaka jedinica skrivenog sloja
prima vagani ulaz iz ulaznog sloja (početne težine su postavljene
slučajno, često u intervalu od -0.1 do 0.1) prema formuli
(Masters, 1993):
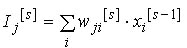
gdje je 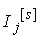 ulaz
u neuron j u sloju s, ulaz
u neuron j u sloju s, 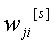 je težina veze od neurona j (u sloju s)
prema neuronu i (u sloju s-1), a
je težina veze od neurona j (u sloju s)
prema neuronu i (u sloju s-1), a 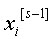 je
ulazna vrijednost koja se šalje iz prethodnog sloja s-1
(slika 5). Npr. ako je skriveni
sloj označen sa s, tada je ulazni sloj označen sa s-1. je
ulazna vrijednost koja se šalje iz prethodnog sloja s-1
(slika 5). Npr. ako je skriveni
sloj označen sa s, tada je ulazni sloj označen sa s-1.
Jedinice u skrivenom sloju prenose svoje ulaze prema formuli:
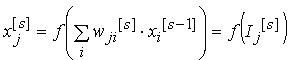
gdje je 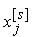 izlaz
neurona j u sloj s, a f je prijenosna
funkcija (sigmoida, tangens-hiperbolna ili neka druga funkcija). izlaz
neurona j u sloj s, a f je prijenosna
funkcija (sigmoida, tangens-hiperbolna ili neka druga funkcija).
Kada ulazni sloj šalje podatke
u prvi skriveni sloj, svaka jedinica skrivenog sloja prima
vagani ulaz iz ulaznog sloja (početne težine su postavljene
slučajno, često u intervalu od -0.1 do 0.1) prema formuli
(Masters, 1993):
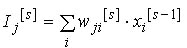
gdje je 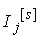 ulaz
u neuron j u sloju s, ulaz
u neuron j u sloju s, 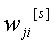 je
težina veze od neurona j prema neuronu i
(u sloju s-1). Jedinice u skrivenom sloju prenose svoje
ulaze prema formuli: je
težina veze od neurona j prema neuronu i
(u sloju s-1). Jedinice u skrivenom sloju prenose svoje
ulaze prema formuli:
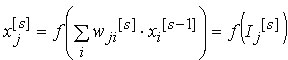
gdje je 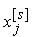 izlaz
neurona j u sloj s, a f je
prijenosna funkcija (sigmoida, tangens-hiperbolna ili neka
druga funkcija). izlaz
neurona j u sloj s, a f je
prijenosna funkcija (sigmoida, tangens-hiperbolna ili neka
druga funkcija).
Ako postoji više od jednog
skrivenog sloja, gore navedena prijenosna funkcija upotrebljava
se kroz sve skrivene slojeve sve dok se ne dostigne izlazni
sloj.
Primjer
2. Primjer mreže tipa backpropagation
Prva neuronska mreža, Perceptron,
čiji je kreator Rosenblatt, sastojala se samo od ulaznog i
izlaznog sloja, te nije mogla aproksimirati funkcije koje
nisu bile linearno djeljive, kao npr. XOR funkciju (vidi primjer
2, gdje mreža tipa širenje unatrag uspješno rješava taj problem).
Problem je riješen tek desetak godina kasnije uvođenjem dodatnog
skrivenog sloja (Werbos, Rumelhart, Hinton, Wiliams), čime
je postignuta nelinearnost u mreži, i dokazano je da su takve
mreže u mogućnosti aproksimirati bilo koju kontinuiranu funkciju.
19.03.2003 |



